QC検定®3級 練習問題　正規分布確率計算

QC検定3級　練習問題（確率・工程能力指数）

A社では長時間の使用を意識したボールペンを製造しています。このボールペンのインクの充填量を測定するために、無作為に標本を30本取り出してみると、平均で1.75ミリリットル、標準偏差は0.02という値を得ました。（尚、母集団は正規分布していると仮定します）

以下の問いに答えなさい。（下へスクロールすると回答例があります）

問１　インクの充填量が1.79ミリリットル以上となる確率は〇〇％と言える。

問２　インクの充填量の規格幅を1.74～1.76ミリリットルとし、Cp（工程能力指数）を1.33にするためには、標準偏差を〇〇にしなければならない。

 

 

 

 

 

 

 

 

 

 

 

 

解答例

問１

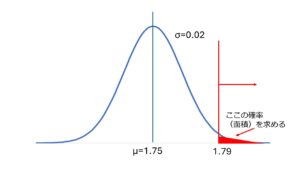
この問題は正規分布の標準化を活用した確率計算です。　この問題の文章から、以下の図を描くことと標準化の公式Kp = X- µ / σを思い出す必要があります。

Kp＝確率変数（平均値からいくつσ分は鳴れているか）

X＝興味のある値

µ＝平均値

σ＝標準偏差

 

 

 

 

 

 

標準化の公式に　Kp = X- µ / σ　に当てはめる

X = 気になる値：1.79ml
µ = 平均値：1.75ml
σ = 標準偏差：0.02ml

• 分子X- µを求めることで、平均値からの距離がわかり、それを分母σでわることで「平均値から何σ分離れているか？」が分かる。これがKp値となる。
• Kp値が分かれば、標準正規分布表から（下記参照）、Kp値の外側が何％の確率なのかを読み取ることができる。
• Kp = 1.79 – 1.75 / 0.02
• Kp = 0.04 / 0.02
• Kp = 2
• 標準正規分布表より、0.02275の値を得ることが出来る。

よって、1.79以上となる確率は、およそ2.23％と言える。

 

正規分布表

	0	0.01	0.02	0.03	0.04	0.05	0.06	0.07	0.08	0.09
0.0	0.50000	0.49601	0.49202	0.48803	0.48405	0.48006	0.47608	0.47210	0.46812	0.46414
0.1	0.46017	0.45620	0.45224	0.44828	0.44433	0.44038	0.43644	0.43251	0.42858	0.42465
0.2	0.42074	0.41683	0.41294	0.40905	0.40517	0.40129	0.39743	0.39358	0.38974	0.38591
0.3	0.38209	0.37828	0.37448	0.37070	0.36693	0.36317	0.35942	0.35569	0.35197	0.34827
0.4	0.34458	0.34090	0.33724	0.33360	0.32997	0.32636	0.32276	0.31918	0.31561	0.31207
0.5	0.30854	0.30503	0.30153	0.29806	0.29460	0.29116	0.28774	0.28434	0.28096	0.27760
0.6	0.27425	0.27093	0.26763	0.26435	0.26109	0.25785	0.25463	0.25143	0.24825	0.24510
0.7	0.24196	0.23885	0.23576	0.23270	0.22965	0.22663	0.22363	0.22065	0.21770	0.21476
0.8	0.21186	0.20897	0.20611	0.20327	0.20045	0.19766	0.19489	0.19215	0.18943	0.18673
0.9	0.18406	0.18141	0.17879	0.17619	0.17361	0.17106	0.16853	0.16602	0.16354	0.16109
1.0	0.15866	0.15625	0.15386	0.15151	0.14917	0.14686	0.14457	0.14231	0.14007	0.13786
1.1	0.13567	0.13350	0.13136	0.12924	0.12714	0.12507	0.12302	0.12100	0.11900	0.11702
1.2	0.11507	0.11314	0.11123	0.10935	0.10749	0.10565	0.10383	0.10204	0.10027	0.09853
1.3	0.09680	0.09510	0.09342	0.09176	0.09012	0.08851	0.08691	0.08534	0.08379	0.08226
1.4	0.08076	0.07927	0.07780	0.07636	0.07493	0.07353	0.07215	0.07078	0.06944	0.06811
1.5	0.06681	0.06552	0.06426	0.06301	0.06178	0.06057	0.05938	0.05821	0.05705	0.05592
1.6	0.05480	0.05370	0.05262	0.05155	0.05050	0.04947	0.04846	0.04746	0.04648	0.04551
1.7	0.04457	0.04363	0.04272	0.04182	0.04093	0.04006	0.03920	0.03836	0.03754	0.03673
1.8	0.03593	0.03515	0.03438	0.03362	0.03288	0.03216	0.03144	0.03074	0.03005	0.02938
1.9	0.02872	0.02807	0.02743	0.02680	0.02619	0.02559	0.02500	0.02442	0.02385	0.02330
2.0	0.02275	0.02222	0.02169	0.02118	0.02068	0.02018	0.01970	0.01923	0.01876	0.01831
2.1	0.01786	0.01743	0.01700	0.01659	0.01618	0.01578	0.01539	0.01500	0.01463	0.01426
2.2	0.01390	0.01355	0.01321	0.01287	0.01255	0.01222	0.01191	0.01160	0.01130	0.01101
2.3	0.01072	0.01044	0.01017	0.00990	0.00964	0.00939	0.00914	0.00889	0.00866	0.00842
2.4	0.00820	0.00798	0.00776	0.00755	0.00734	0.00714	0.00695	0.00676	0.00657	0.00639
2.5	0.00621	0.00604	0.00587	0.00570	0.00554	0.00539	0.00523	0.00508	0.00494	0.00480

 

問２

工程能力指数Cpの求め方は　Cp = USL – LSL / σ 　：上限規格値 – 下限規格値 / 標準偏差です。

この問題において、上限規格値：1.76、下限規格値：1.74が分かっているので、公式に代入して、σを求める。

Cp(1.33) = 1.76 – 1.74 / σ

1.33 = 0.02 / σ

1.33σ = 0.02

σ = 0.015

検算してみます。　1.76 – 1.74 / 0.015 = 1.33ですから、標準偏差は0.015となります。